放在最前面

题目来自广州大学机器学习实验
本文以解决数据集处理问题为最高目标，不会对涉及到的知识过多介绍，会写出问题解决思路方式
实验题目

基于Adult数据集，完成关于收入是否大于50K的逻辑回归分类、朴素贝叶斯模型训练、测试与评估。
1 准备数据集并认识数据
下载Adult数据集
http://archive.ics.uci.edu/ml/datasets/Adult
了解数据集各个维度特征及预测值的含义
2 探索数据并预处理数据
观察数据集各个维度特征及预测值的数值类型与分布
预处理各维度特征
3 训练模型
编程实现训练数据集上逻辑回归模型的梯度下降参数求解、朴素贝叶斯参数统计
4 测试和评估模型
在测试数据集上计算所训练模型的准确率、AUC等指标

实验内容及步骤

数据集下载处理

http://archive.ics.uci.edu/ml/datasets/Adult

下载后用excel打开文件，发现没有index没有列名，只好手动处理添加一下，处理好的文件我会放在源码文件夹里。

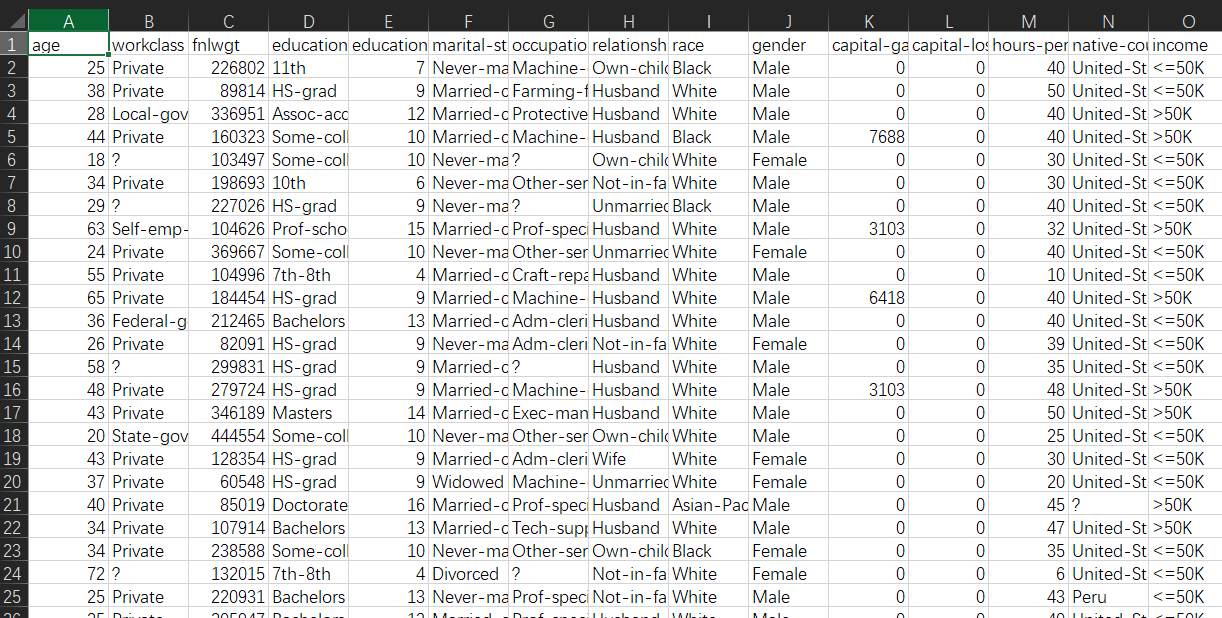
使用pandas读取文件,简单处理一下

# 读取数据,预处理
df = pd.read_csv('adult.csv') 
#去掉含有nan的行
df=df.dropna(axis=0,how='any')

观察数据发现,有些地方有缺省值,用”?”表示,我们需要去掉这些含有问号的行

#预处理，去掉缺省属性的行
df=df[~df['workclass'].isin(["?"])]
df=df[~df['native-country'].isin(["?"])]
df=df[~df['occupation'].isin(["?"])]

因为是要分类收入大于50K和小于等于50K的,我们直接处理一下,将大于50k的设为1,小于等于50k的设为0,放在新的一个列,列名target

#将结果转为二分类值为0 1方便后续处理。重命名为target列
df.loc[df['income'] == ">50K","target"] = 1
df.loc[df['income'] != ">50K","target"] = 0
df.drop(['income'], axis=1 ,inplace=True)

1.逻辑回归分类

继续往下面看前建议先执行了解一下逻辑回归是什么东西,这里不再细说展开,直接写代码

预处理完之后,与朴素贝叶斯不同
我们还需要将离散型特征和连续性特征筛选出来,进行处理

#选出离散型特征
cat_columns = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 
               'gender','native-country']
#连续性特征
num_columns = ['age','fnlwgt','educational-num','capital-gain', 'capital-loss', 'hours-per-week']
#目标特征
target_column = "target"
#对离散型特征独热编码
encoded_df = pd.get_dummies(df,columns=cat_columns)

#特征值
df_x = encoded_df.drop(columns="target")
#目标值
df_y = encoded_df["target"].values

然后把连续型特征的值归一化

#将连续型特征值归一化
num_mean = df_x[num_columns].mean()
num_std = df_x[num_columns].std()
num_normol = (df_x[num_columns] - num_mean)/num_std
df_x.drop(columns=num_columns,inplace=True)
df_x = pd.concat([df_x,num_normol],axis=1).values

然后就可以划分训练集和测试集了,使用sklearn的库划分

#划分训练集测试集
from sklearn.model_selection import StratifiedShuffleSplit
sss = StratifiedShuffleSplit(n_splits=2,train_size=0.7)
for train_index,test_index in sss.split(df_x,df_y):
    trainx,testx = df_x[train_index],df_x[test_index]
    trainy,testy = df_y[train_index],df_y[test_index]

接下来我们就要着手实现逻辑回归了,不了解逻辑回归的强烈建议先执行学习一下

实现sigmoid函数

1
2
3

#sigmoid函数
def sigmoid(x):
  return 1 / (1 + np.exp(-x))

梯度下降法的逻辑回归实现

X=trainx
Y=np.reshape(trainy, (-1, 1))
X_test=testx
Y_test=np.reshape(testy, (-1, 1))
# print(X.shape)
# print (Y.shape)

theta=np.zeros(shape=[1,X.shape[1]])
b=0
#设置学习速率
alpha= 0.001
#学习次数
learning_count =1000
theta = np.zeros(shape=[1, X.shape[1]])
theta = theta.T
for i in range(learning_count):
    pre = np.dot(X, theta)
    w = 1 / (1 + np.exp(-pre))  
    h = np.dot(X.T, (Y - w))  
    h = h / len(h)
    lost = -(np.dot(Y.T, np.log(w)) + np.dot((1 - Y).T, np.log(1 - w))) / len(Y)
    theta = theta + alpha * h
    if i%10000==0:
      print ('梯度下降中...')


y_pre= np.dot(X_test,theta)+b
y_preSigmd=sigmoid(y_pre)

这样求出的预测值并不能直接和测试值比较,我们以0.5划分是0是1

1	y_preSigmd= np.where(y_preSigmd>0.5,1,0)

好这样y_preSigmod里就是我们根据测试集预测出来的值

计算一下准确率

1 2	from sklearn.metrics import accuracy_score print("准确率：",accuracy_score(y_preSigmd, Y_test))

AUC值:

1
2
3

from sklearn.metrics import roc_auc_score
auc_score = roc_auc_score(Y_test,y_preSigmd)
print("AUC值:",auc_score)

2.朴树贝叶斯分类

预处理完之后,与逻辑回归不同,我们需要着重处理连续型特征,将其划分为几个区间特征

#将连续型特征划分区间
df['age']=pd.cut(df['age'],bins=10,right=True)
df['capital-gain']=pd.cut(df['capital-gain'],bins=3,right=True)
df['capital-loss']=pd.cut(df['capital-loss'],bins=3,right=True)
df['hours-per-week']=pd.cut(df['hours-per-week'],bins=20,right=True)
df['fnlwgt']=pd.cut(df['fnlwgt'],bins=20,right=True)

其他本身就已是离散型的特征就不需要处理了

继续划分训练集和测试集

#划分训练集和测试集,设置变量,为下面训练做准备
train_data=df.sample(frac=0.7, random_state=0,axis=0)
test_data=df[~df.index.isin(train_data.index)]

df_x = df.drop(columns="target")
df_y = df["target"].values

trainX=train_data.drop(columns="target")
trainY=train_data['target']
testX=test_data.drop(columns="target")
testY=test_data['target']

接下来我们需要实现朴树贝叶斯,以下代码来自他人之手,进行了完善修改

class NaiveBayes(object):
    def __init__(self, X_train, y_train):
        self.X_train = X_train  #样本特征
        self.y_train = y_train  #样本类别
        #训练集样本中每个类别(二分类)的占比，即P(类别)，供后续使用
        self.P_label = {1: np.mean(y_train.values), 0: 1-np.mean(y_train.values)}
 
    #在数据集data中, 特征feature的值为value的样本所占比例
    #用于计算P(特征|类别)、P(特征)
    def getFrequency(self, data, feature, value):
        num = len(data[data[feature]==value]) #个数
        return num / (len(data))
 
    def predict(self, X_test):
        self.prediction = [] #预测类别
        # 遍历样本
        for i in range(len(X_test)):
            x = X_test.iloc[i]      # 第i个样本
            P_feature_label0 = 1    # P(特征|类别0)之和
            P_feature_label1 = 1    # P(特征|类别1)之和
            P_feature = 1           # P(特征)之和
            # 遍历特征
            for feature in X_test.columns:
                # 分子项，P(特征|类别)
                data0 = self.X_train[self.y_train.values==0]  #取类别为0的样本
                P_feature_label0 *= self.getFrequency(data0, feature, x[feature]) #计算P(feature|0)
 
                data1 = self.X_train[self.y_train.values==1]  #取类别为1的样本
                P_feature_label1 *= self.getFrequency(data1, feature, x[feature]) #计算P(feature|1)
 
                # 分母项，P(特征)
                P_feature *= self.getFrequency(self.X_train, feature, x[feature])
 
            #属于每个类别的概率
            if i%25==0:
                # print ('...')
                print("预测第",i,"个")
                print(P_feature_label0)
                print(P_feature_label1)
            P_0 = (P_feature_label0*self.P_label[0]) / P_feature
            P_1 = (P_feature_label1 * self.P_label[1]) / P_feature
            #选出大概率值对应的类别
            self.prediction.append([1 if P_1>=P_0 else 0])
        return self.prediction
#from https://blog.csdn.net/weixin_39710249/article/details/111373540

调用该类训练预测

1
2
3

model = NaiveBayes(trainX, trainY)  
y_pre = model.predict(testX)    
print(y_pre)

计算准确率:

1 2	from sklearn.metrics import accuracy_score print("准确率：",accuracy_score(y_pre, testY))

计算auc值:

#auc值
from sklearn.metrics import roc_auc_score
auc_score = roc_auc_score(testY,y_pre)
print("AUC值:",auc_score)

源码文件

Github

机器学习实验朴素贝叶斯逻辑回归处理adult数据集(附代码)