放在前面
- 来自广州大学人工智能实验
- 仅记录代码实现过程思路,不对涉及知识过多讲解
遗传算法解决旅行商问题
一 对旅行商问题进行编码
旅行商问题,目标是求一个走过所有目标地点尽量最短的路径。我们可以将这个路径视为一个数组,数组中的每个元素就是经过的城市的编号,元素的排列顺序就是走过地点的顺序。
以遗传算法的视角来看,该数组(路径)中的元素相当于基因,但是这个基因并不重复,因为旅行商问题不会重复走过同一个地点。
所以我们可以将每一条路径视为一个数组,数组中的元素就是地点。种群由这些一条条不同的数组(路径)组成。
在QT中可以用以下这种方式存储路径,元素int类型可以是地点的编号
不过我们还是得创建一个location类,将地点信息(名称,坐标等)存储一下,方便后面操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#ifndef LOCATION_H
#define LOCATION_H
#include <QObject>
#include<QtDebug>
class location
{
private:
int X;
int Y;
int code;
public:
location();
location(int code,int X,int Y);
void qdebugLocation();
int getX();
int getY();
int getCode();
};
#endif
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
location::location(int code,int X,int Y){
this->X=X;
this->Y=Y;
this->code=code;
}
int location::getX()
return this->X;
int location::getY()
return this->Y;
int location::getCode()
return this->code;
|
然后可以用QVector存储所有地点信息
二 遗传算法函数实现
TSP的遗传算法总体思路:
- a)随机生成N个不同的路径数个体,组成初始种群
- b)使用锦标赛选择策略从种群中选择出新的个体,组成新的交配池
- c)从交配池中随机选择出两个个体,根据交配概率PC交配
- d)如果交配则交配后按照变异概率PM进行变异,不交配直接放入新种群
- e)重复b-d步骤
我们创建一个GA类来实现TSP的遗传算法,头文件如下
后面会仔细讲解每个函数的作用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#ifndef GA_H
#define GA_H
#include "location.h"
#include <QVector>
#include<QRandomGenerator>
#include<QDebug>
class GA
{
public:
GA();
void init_races(int size,int num);
double getPathLength(QVector<int>path, int num);
void tournament(int size,int num);
void getRandomSwitchPoint (int &p1, int &p2,int size);
void crossover(int size,int num,double pc,double pm);
void removeDuplicates(QVector<int> &path_1, QVector<int> &path_2);
void mutations(QVector<int>&path,int num);
double getMinPathInPool(int num,QVector<int> &minPath);
QString outputPath(QVector<int> path);
void debugPool();
void debugPath(QVector<int> path);
private:
QVector<location> loc;
QVector<QVector<int>>* pool=nullptr;
QVector<int> minPath;
};
#endif
|
1.初始化位置信息
我们在GA的构造函数中编写添加位置信息的代码,这样我们新建GA对象后就已经有位置信息了,在ga.cpp文件中编写代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
GA::GA()
{
loc.append(location(1,87,7));
loc.append(location(2,91,38));
loc.append(location(3,83,46));
loc.append(location(4,71,44));
loc.append(location(5,64,60));
loc.append(location(6,68,58));
loc.append(location(7,83,69));
loc.append(location(8,87,76));
loc.append(location(9,74,78));
loc.append(location(10,71,71));
loc.append(location(11,58,62));
loc.append(location(12,54,62));
loc.append(location(13,51,67));
loc.append(location(14,37,84));
loc.append(location(15,41,94));
loc.append(location(16,2,99));
loc.append(location(17,7,64));
loc.append(location(18,22,60));
loc.append(location(19,25,62));
loc.append(location(20,18,54));
loc.append(location(21,4,50));
loc.append(location(22,13,40));
loc.append(location(23,18,40));
loc.append(location(24,24,42));
loc.append(location(25,25,38));
loc.append(location(26,41,26));
loc.append(location(27,45,35));
loc.append(location(28,44,35));
loc.append(location(29,58,35));
loc.append(location(30,62,32));
}
|
我们把这些信息写入到QVector<int>
这个位置信息当然是根据给的题目要求来的,参数分别是 地点编号,X坐标,Y坐标。
2.生成初始种群
a)随机生成N个不同的路径数个体,组成初始种群
遗传算法第一步就是要生成初始随机种群,思路上面讲了,生成给定种群大小为NUM个的随机不同路径,个体用QVector<int>表示,元素int代表地点编号。
可以使用启发性的方法生成初始种群,不过我这里就用最简单较差的方法了,直接随机生成。
我们可以随机生成SIZE个小于SIZE值的int值存储到到这个QVector<int>里(SIZE值就是要走过的地点数,个体的基因数)。
举个例子:
1
2
3
4
| QVector<int> path ={0,4,1,3,2}
|
个体路径的表示方法我们解决了,另外我们还需要还要一个变量pool种群来存储全部生成的个体,我们可以写一个QVector<QVector<int>>指针,然后作为GA的私有成员,这样就能方便我们后续迭代,如下:
1
2
|
QVector<QVector<int>>* pool=nullptr;
|
明白之后我们来看如何实现随机初始种群,直接放上代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
void GA::init_races(int size,int num)
{
Q_ASSERT(this->pool==nullptr);
this->pool=new QVector<QVector<int>>;
for(int i=0;i<size;i++){
QVector<int> now;
int tmprand;
QVector<bool> tmp(num,false);
for(int k=0;k<num;k++){
do{
tmprand=QRandomGenerator::securelySeeded().bounded(num)
}
while (tmp.at(tmprand)==true);
tmp[tmprand]=true;
now.append(tmprand);
}
this->pool->append(now);
}
}
|
主要用到了QRandomGenerator这个类,这个是QT5.10之后加进来的,可以不需要自己另外设种子了(当然你也可以设),官方文档:QRandomGenerator Class
初始化好的种群在pool指针里了
2.计算适应值(计算路径长度)
在开始选择子代之前,我们需要实现一个函数用于计算适应值判断个体对于目标的适应值高低,从而有方向地选择子代个体。
在TSP问题中计算适应值就变成了计算路径长度之和了。代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| double GA::getPathLength(QVector<int>path, int num)
{
qDebug()<<"getpathlength";
Q_ASSERT(num==path.size());
double pathLength=0;
for(int k=0;k<path.size()-1;k++){
pathLength+=sqrt(pow(qAbs((this->loc[path[k]].getX())-(this->loc[path[k+1]].getX())),2)+pow(qAbs((this->loc[path[k]].getY())-(this->loc[path[k+1]].getY())),2));
}
pathLength+=sqrt(pow(qAbs((this->loc[path.last()].getX())-(this->loc[path.first()].getX())),2)+pow(qAbs((this->loc[path.last()].getY())-(this->loc[path.first()].getY())),2));
qDebug()<<"nowpath:"<<pathLength;
return pathLength;
}
|
计算距离有两种方式,依据题目要求使用欧氏距离或曼哈顿距离,这里使用的是欧氏距离。另外注意有些题目要求是要从最后一个城市回到最初城市,所以还得加上这个距离。
3.筛选出交配池
b)使用锦标赛选择策略从种群中选择出新的个体,组成新的交配池
其实筛选个体的方法除了锦标赛算法还有一个轮盘赌算法选择的方法,不过这里用的是锦标赛算法,轮盘赌算法就不介绍了,有兴趣可以自行了解。
遗传算法中的锦标赛选择策略每次从种群中取出一定数量个体(放回抽样),然后选择其中最好的一个进入子代种群。重复该操作,直到新的种群规模达到原来的种群规模。几元锦标赛就是一次性在总体中取出几个个体,然后在这些个体中取出最优的个体放入保留到下一代种群的集合中。
这里我们采用二元锦标赛,每次选出两个(放回)进行比较路径长度大小,将较小的的路径加入到新交配池子
直接看代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| void GA::tournament( int size,int num)
{
qDebug()<<"tournament";
Q_ASSERT(size>0);
QVector<QVector<int>> *newpool=new QVector<QVector<int>>;
int time=size;
while(time--){
int index_1=QRandomGenerator::system()->bounded(size);
int index_2=QRandomGenerator::system()->bounded(size);
if(getPathLength(this->pool->at(index_1),num)<getPathLength(this->pool->at(index_2),num)){
newpool->append(this->pool->at(index_1));
}else{
newpool->append(this->pool->at(index_2));
}
}
delete this->pool;
this->pool=newpool;
debugPool();
}
|
4.进行交配和变异
c)从交配池中随机选择出两个个体,根据交配概率PC交配
d)如果交配则交配后按照变异概率PM进行变异,不交配直接放入新种群
这一步我们需要随机选出两个个体,根据交配概率PC判断是否进行交配,如果不交配,那我们直接将这两个个体放入新种群(交配池)即可;如果交配,则要进行交配策略,进行交配策略之后还要根据变异概率PM是否进行变异
遗传算法中如何进行交配呢? 常用的策略方法有一点交叉和两点交叉
交叉的步骤如下:
1.从交配池中随机选出两个个体作为需要交叉的个体
2.根据个体基因长度SIZE,随机生成一个或多个范围在[0,size-1]的整数下标点作为交叉点
3.交换两个个体由交叉点指定的基因范围部分‘
一点交叉:
就是只选择一个交叉点进行交换
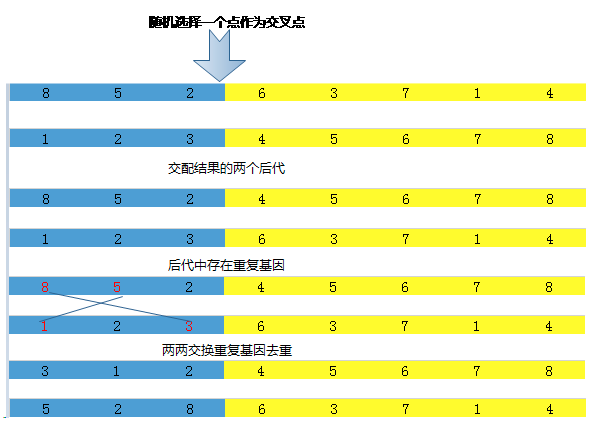
两点交叉:
两个交叉点,将两个交叉点之间的基因部分交换
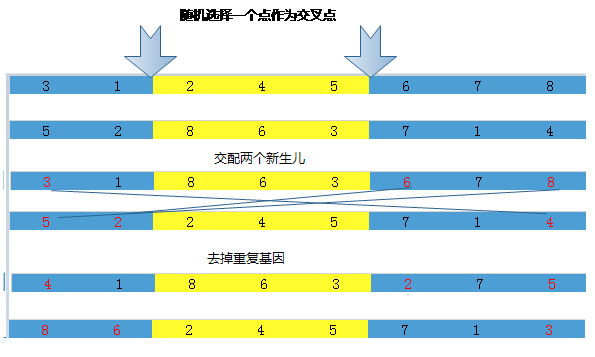
要注意的是,交换后会出现部分基因重复,也就是地点重复,这是不允许的,所以我们要去掉重复地点
方法很简单,分别找到两个个体中重复的部分,然后互相交换即可。
然后再说说变异,变异在tsp问题中我们用一种简单的方法进行处理:随机交换一个个体中两个基因的位置。
也就是随机选取两个地点交换在路径中的位置
例如:1->2->3->4
可以变异为 1->4->3->2(交换了2和4的位置)
理解后我们就可以写代码了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
|
void GA::getRandomSwitchPoint(int &p1,int &p2,int num)
{
int tmp1,tmp2;
do{
tmp1=QRandomGenerator::system()->bounded(num);
tmp2=QRandomGenerator::system()->bounded(num);
}while(tmp1>=tmp2&&!((tmp2-tmp1)>=2));
p1=tmp1;
p2=tmp2;
}
void GA::removeDuplicates(QVector<int> &path_1, QVector<int> &path_2)
{
qDebug()<<"removeDuplicates";
QVector<int> duplicates_1;
for(auto i=path_1.begin();i!=path_1.end();i++){
if(path_1.count(*i)>1){
if(duplicates_1.contains(*i)==false)
duplicates_1.append(*i);
}
}
QVector<int> duplicates_2;
for(auto i=path_2.begin();i!=path_2.end();i++){
if(path_2.count(*i)>1){
if(duplicates_2.contains(*i)==false)
duplicates_2.append(*i);
}
}
if(duplicates_1.size()>0){
debugPath(duplicates_1);
debugPath(duplicates_2);
Q_ASSERT(duplicates_1.size()==duplicates_2.size());
for(int i=0;i<duplicates_1.size();i++){
int tmp= path_1[path_1.indexOf(duplicates_1[i])];
path_1[path_1.indexOf(duplicates_1[i])]=duplicates_2[i];
path_2[path_2.indexOf(duplicates_2[i])]=tmp;
}
debugPath(path_1);
debugPath(path_2);
}
}
void GA::crossover(int size,int num,double pc,double pm)
{
Q_ASSERT(this->pool->size()>0);
Q_ASSERT(size>0&&num>0);
Q_ASSERT(pc>=0&&pc<=1);
QVector<QVector<int>>* newPool=new QVector<QVector<int>>;
int time=size;
while (time--) {
int rand_1=QRandomGenerator::system()->bounded(size);
int rand_2=QRandomGenerator::system()->bounded(size);
QVector<int> tmpPath_1=this->pool->at(rand_1);
QVector<int> tmpPath_2=this->pool->at(rand_2);
debugPath(tmpPath_1);
debugPath(tmpPath_2);
double randPC=double(QRandomGenerator::system()->bounded(1.0));
qDebug()<<"randpc:"<<randPC;
Q_ASSERT(randPC<1&&rand()>=0);
if(randPC>pc){
qDebug()<<"不交配";
newPool->append(tmpPath_1);
newPool->append(tmpPath_2);
}else{
qDebug()<<"交配";
int crossPos_1,crossPos_2;
getRandomSwitchPoint(crossPos_1,crossPos_2,num);
Q_ASSERT(crossPos_2>crossPos_1);
for(int i=crossPos_1;i<crossPos_2;i++){
int tmppp=tmpPath_1[i];
tmpPath_1[i]=tmpPath_2[i];
tmpPath_2[i]=tmppp;
}
debugPath(tmpPath_1);
debugPath(tmpPath_2);
removeDuplicates(tmpPath_1,tmpPath_2);
double randPM=double(QRandomGenerator::system()->bounded(1.0));
if(randPM<pm){
qDebug()<<"mutations";
mutations(tmpPath_1,num);
mutations(tmpPath_2,num);
debugPath(tmpPath_1);
debugPath(tmpPath_2);
}
newPool->append(tmpPath_1);
newPool->append(tmpPath_2);
}
}
delete pool;
pool=newPool;
}
inline void GA::mutations(QVector<int> &path,int num)
{
int randIndex_1=QRandomGenerator::system()->bounded(num);
int randIndex_2=QRandomGenerator::system()->bounded(num);
if(randIndex_1!=randIndex_2){
int tmp=path[randIndex_1];
path[randIndex_1]=path[randIndex_2];
path[randIndex_2]=tmp;
}
}
|
这样遗传算法对于TSP问的的实现就基本写好了
接下来我们设计个可视化界面,方便我们查看遗传算法不同参数对于结果的影响
三 设计可视化界面
目标:
1.可以设定PM概率,PC概率,种群大小和迭代次数
2.结果用折线图显示,方便查看
1.设计.ui文件
简单设计一下即可,留出给设置变量的lineEdit组件,下面是我设计的界面
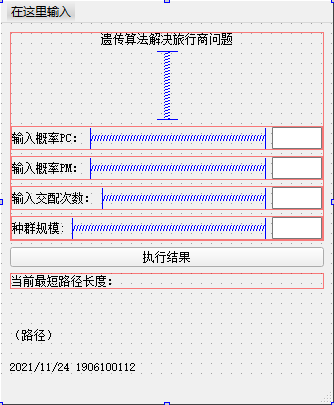
在文本框输入参数值,点击执行结果按钮计算结果,能够将结果中的最短路径长度和路径显示出来,也能显示耗时
2.实现显示折线图
QT中有提供实现相关视图的类,要实现折线图需要用到下面几个头文件:
1
2
3
4
| #include <QLineSeries>
#include <QValueAxis>
#include <QChartView>
#include <QChart>
|
在这里不对使用的类做过多介绍,可以自行查看QT官方文档,大概用法如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| QLineSeries *series = new QLineSeries()
series->append(X,Y);
QChart *chart = new QChart();
chart->legend()->hide();
chart->createDefaultAxes();
chart->setTitle("XXX");
QValueAxis *aX=new QValueAxis;
QValueAxis *aY=new QValueAxis;
aX->setTitleText("次数");
aX->setLabelFormat("%d");
aX->setTitleVisible(true);
aY->setTitleVisible(true);
aY->setLabelFormat("%d");
aY->setTitleText("路径长度");
chart->addAxis(aX,Qt::AlignBottom);
chart->addAxis(aY,Qt::AlignLeft);
chart->addSeries(series);
series->attachAxis(aX);
series->attachAxis(aY);
QChartView *chartView = new QChartView(chart);
chartView->setRenderHint(QPainter::Antialiasing);
QMainWindow *chartV=new QMainWindow;
chartV->setCentralWidget(chartView);
chartV->resize(800, 500);
chartV->show();
|
3.按钮槽函数编写
这部分应该不用多说了,给“执行按钮”写一个信号为点击的槽函数,然后执行遗传算法,不用多说直接上代码吧,这里也直接把上一步折线图的实现写进来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include "mainwindow.h"
#include "ui_mainwindow.h"
QT_CHARTS_USE_NAMESPACE
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
ui->setupUi(this);
ui->cycleEdit->setText("100");
ui->pcEdit->setText("0.5");
ui->pmEdit->setText("0.3");
ui->sizeEdit->setText("20");
}
MainWindow::~MainWindow()
{
delete ui;
}
void MainWindow::on_resultBtn_clicked()
{
try {
int size=ui->sizeEdit->text().toInt();
double pc=ui->pcEdit->text().toDouble();
double pm=ui->pmEdit->text().toDouble();
int cycletime=ui->cycleEdit->text().toInt();
if(size<=0||pc<=0||pm<=0||cycletime<=0){
qDebug()<<"out";
throw QString("输入值非法");
}
GA tsp;
int path;
tsp.init_races(size,30);
QLineSeries *series = new QLineSeries();
int minPathGlobalValue=INT32_MAX;
QVector<int> minPathGlobal;
QTime cTime;
cTime.start();
int time=cycletime;
while(time--){
tsp.tournament(size,30);
tsp.crossover(size,30,pc,pm);
QVector<int> minPath;
path=tsp.getMinPathInPool(30,minPath);
series->append(cycletime - time,path);
if(path<minPathGlobalValue){
minPathGlobalValue=path;
minPathGlobal=minPath;
}
qDebug()<<"PATH:"<<path;
}
int runtime=cTime.elapsed();
ui->runtime->setText(QString("花费时间:%1ms").arg(runtime));
ui->pathValue->setText(QString::number(minPathGlobalValue));
ui->path->setText(tsp.outputPath(minPathGlobal));
QChart *chart = new QChart();
chart->legend()->hide();
chart->createDefaultAxes();
chart->setTitle(QString("遗传算法解决旅行商问题 PC:%1 PM:%2 种群规模:%3").arg(pc).arg(pm).arg(size));
QValueAxis *aX=new QValueAxis;
QValueAxis *aY=new QValueAxis;
aX->setTitleText("次数");
aX->setLabelFormat("%d");
aX->setTitleVisible(true);
aY->setTitleVisible(true);
aY->setLabelFormat("%d");
aY->setTitleText("路径长度");
chart->addAxis(aX,Qt::AlignBottom);
chart->addAxis(aY,Qt::AlignLeft);
chart->addSeries(series);
series->attachAxis(aX);
series->attachAxis(aY);
QChartView *chartView = new QChartView(chart);
chartView->setRenderHint(QPainter::Antialiasing);
QMainWindow *chartV=new QMainWindow;
chartV->setCentralWidget(chartView);
chartV->resize(800, 500);
chartV->show();
} catch (QString warningInfo) {
QMessageBox::warning(this,"警告",warningInfo);
}
}
|
这样就完成了:使用QT实现遗传算法处理旅行商问题
程序完整源码我会放在文章后面
四 运行结果
主界面
点击”执行结果”执行遗传算法
视给定的参数不同,耗时也不同
计算完会弹出一个窗口
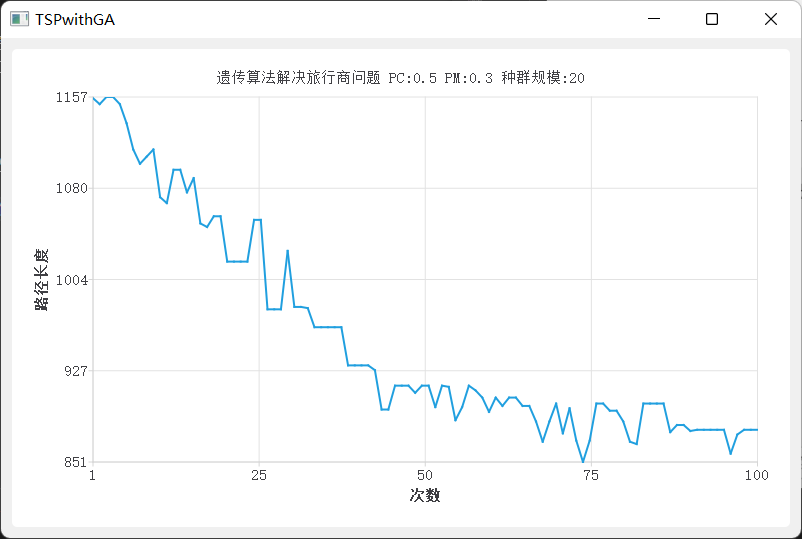
然后主界面也会更新
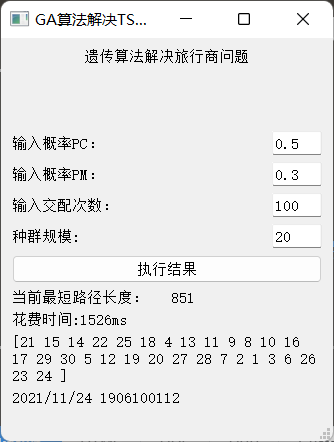
我所设定的地点信息的最短路径其实是按城市编号从小到大的顺序为最短。最短路径为415左右,可以看到这遗传算法执行出来的结果还是差距蛮大的,接下来我们换几个参数看看。
- PC= 0.7 PM=0.1 size=20
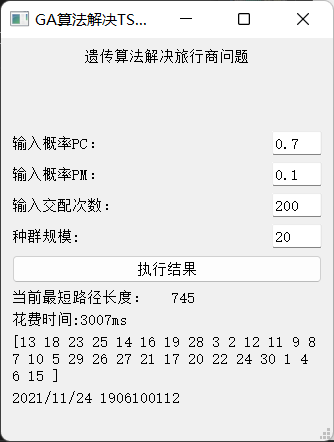
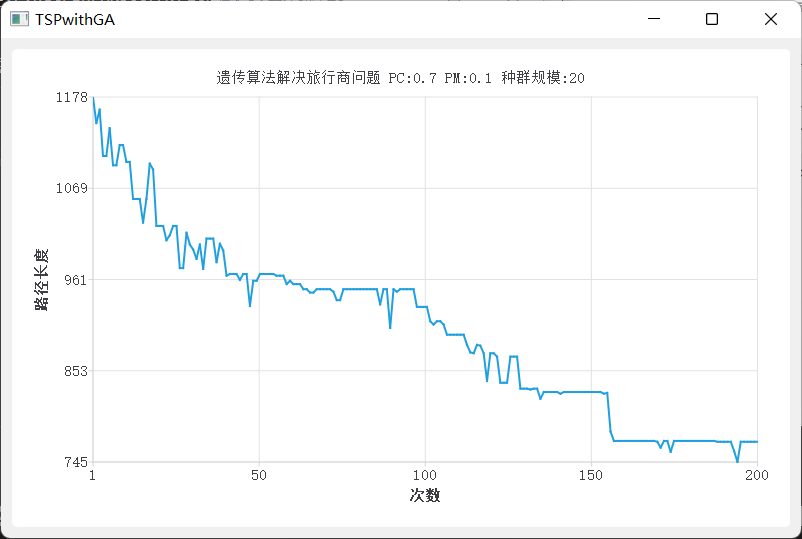
- PC= 0.7 PM=0.1 size=20 time=200
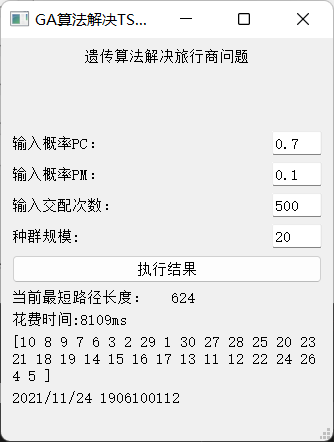
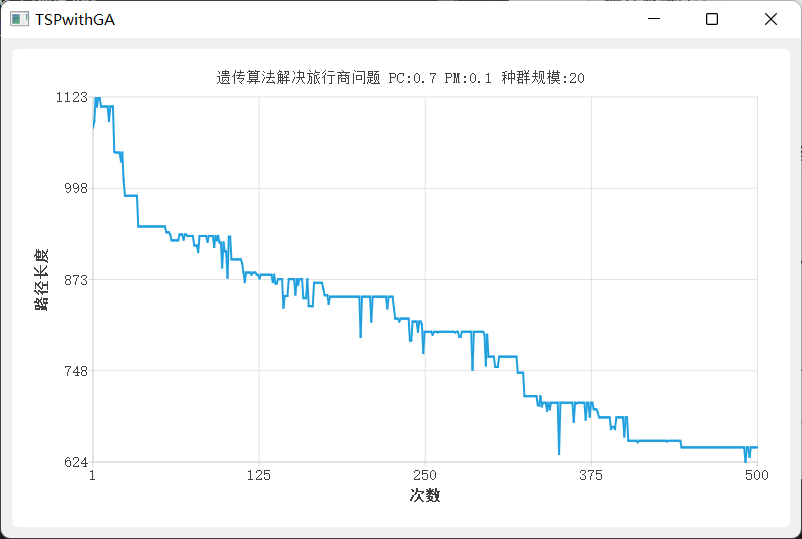
- PC= 0.8 PM=0.2 size=20 time=1000
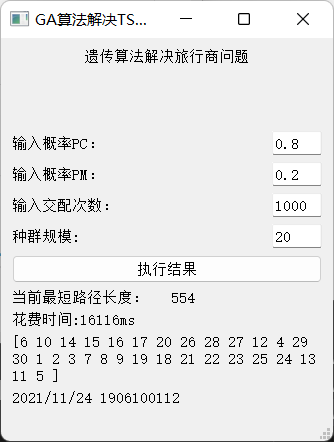
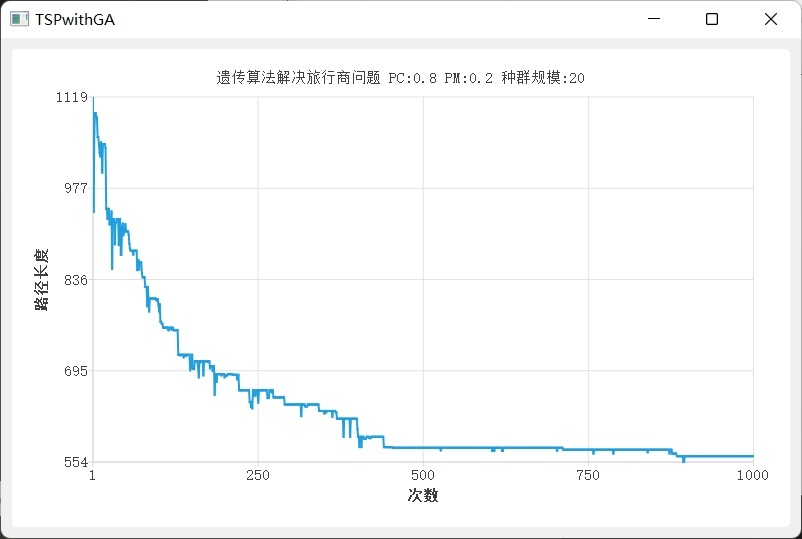
不同参数对计算结果影响也不同,参数的选择也是遗传算法比较关键的地方。
结尾
作为学校人工智能的实验之一,遗传算法解决TSP问题让我又学到了不少算法相关的东西,还新接触了QT的图表类,收获颇多。也让我对TSP问题又多了一丝兴趣,而遗传算法本身也十分有趣,运用基因遗传仿生学来作为算法也是令人惊讶赞叹不已。
Reference:
项目源码:Github